國立板橋高級中學九十九學年度第一學期第二次期中考高一數學試題卷

                                                  

一、單選題：每題 6 分，共計 30 分。

 

1.設為實係數三次多項式，則下列何者錯誤？

(A)方程式必有實根                (B)方程式必有實根    

(C)方程式必有實根          (D)方程式必有實根     (E)方程式必有

Ans：D  [解說]  [試題分析]

 

 

2.下列選項中何者的值最大？

(A)      (B)      (C)      (D)    (E)

Ans：C  [解說]  [試題分析]

 

 

 

3.若實係數二次方程式有一實根，且，則的最大值為何？

(A)       (B)       (C)       (D)    (E)

Ans：B  [解說]  [試題分析]

 

 

 

4.已知是實係數方程式的兩實根，求的最小值？

(A)       (B)       (C)       (D)

Ans：C  [解說]  [試題分析]

 

 

 

5.設，

5.(其中均為實數)，若，，，，試問下列何者錯誤？

(A)        (B)        (C)       (D)

Ans：D  [解說]  [試題分析]

 

 

 

 

二、多選題：每題至少有一個選項是正確的，每題全部答對得 10 分，錯一個得 6 分，錯兩個得 2 分，錯三個或三個以上不給分，整題未作答，亦不給分，共計 20 分。

 

1.設為整係數多項式，且複數為方程式的一根，試問下列敘述哪些正確？

(A)複數可能為方程式的一根

(B)的各項係數和必為偶數

(C)若，則

(D)若除以的餘式為，則方程式恰有三個實根

(E)若，則方程式至少有二個負根

Ans：BDE  [解說]  [試題分析]

 

 

 

2.設是不為的複數，試問下列敘述哪些正確？

(A)若是整數，則不一定是整數

(B)若是有理數，則必是有理數

(C)若的實部與的實部兩者的乘積小於，則必不為實數

(D)若的虛部與的虛部均為正數，則必大於

(E)若是方程式的虛根，則是方程式的實根

Ans：CDE  [解說]  [試題分析]

 

 

 

 

三、填充題：每題 6 分，共計 42 分。

 

1.求的值為　　　　　。

Ans：  [解說]  [試題分析]

 

 

 

2.不等式的解為　　　　　。

Ans：或  [解說]  [試題分析]

 

 

 

3.設，試求的值為　　　　　。

Ans：4  [解說]  [試題分析]

 

 

 

4.設為實數，若不等式無實數解，則的範圍為　　　　　。

Ans：  [解說]  [試題分析]

 

 

 

5.設，則的解為　　　　　。

Ans：  [解說]  [試題分析]

 

 

 

6.設，則除以的餘式為　　　　　。

Ans：3  [解說]  [試題分析]

 

 

 

7.設多項式除以的餘式為，除以的餘式為，試求除以的餘式為　　　　　。

Ans：  [解說]  [試題分析]

 

 

 

 

四、計算題：第 1 題答對得 3 分，第 2 題答對得 5 分，共計 8 分。

 

如圖，已知二次函數的圖形與軸交於,兩點，其中為頂點，且與的面積相等，

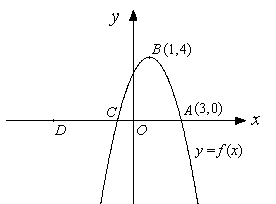試求：(1)若點的坐標為，其中，則？

Ans：  [解說]  [試題分析]

 

 

 

 

 

 

 

試求：(2)承上，若過,,,四點的最低次多項式函數為，則？

Ans：  [解說]  [試題分析]